Mastering The Art Of Graphing The Inverse Function
Understanding how to graph the inverse function is a fundamental skill that every math enthusiast should possess. Inverse functions play a crucial role in various applications, ranging from algebra to calculus, and even in real-world scenarios. The ability to graph these functions not only enhances one's understanding of mathematical concepts but also facilitates problem-solving skills. In this article, we will delve into the intricacies of graphing inverse functions, providing a comprehensive guide that is both informative and engaging.
Whether you are a student looking to improve your mathematical prowess or a teacher seeking effective ways to explain this concept, mastering how to graph the inverse function will serve you well. We will explore the essential steps involved in graphing these functions, discuss common challenges, and provide tips for success. By the end of this guide, you will have the knowledge and confidence needed to tackle any problem related to inverse functions.
So, why is it important to graph the inverse function? Graphing these functions allows us to visualize the relationship between two variables and understand their behavior. This understanding is crucial for solving equations, analyzing data, and even in fields such as physics and engineering. Join us as we take a deep dive into the world of inverse functions and learn how to graph them effectively!
What is an Inverse Function?
An inverse function essentially reverses the effect of the original function. If you have a function f(x) that takes an input x and produces an output y, the inverse function, denoted as f-1(y), will take that output y and return it to the original input x. In mathematical terms, if f(x) = y, then f-1(y) = x.
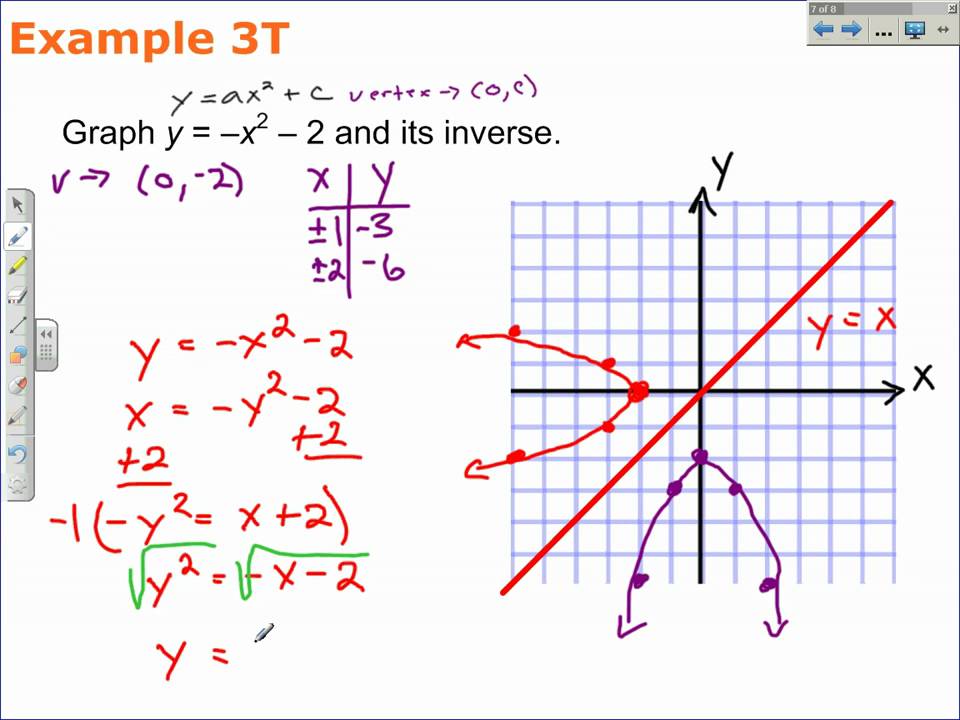
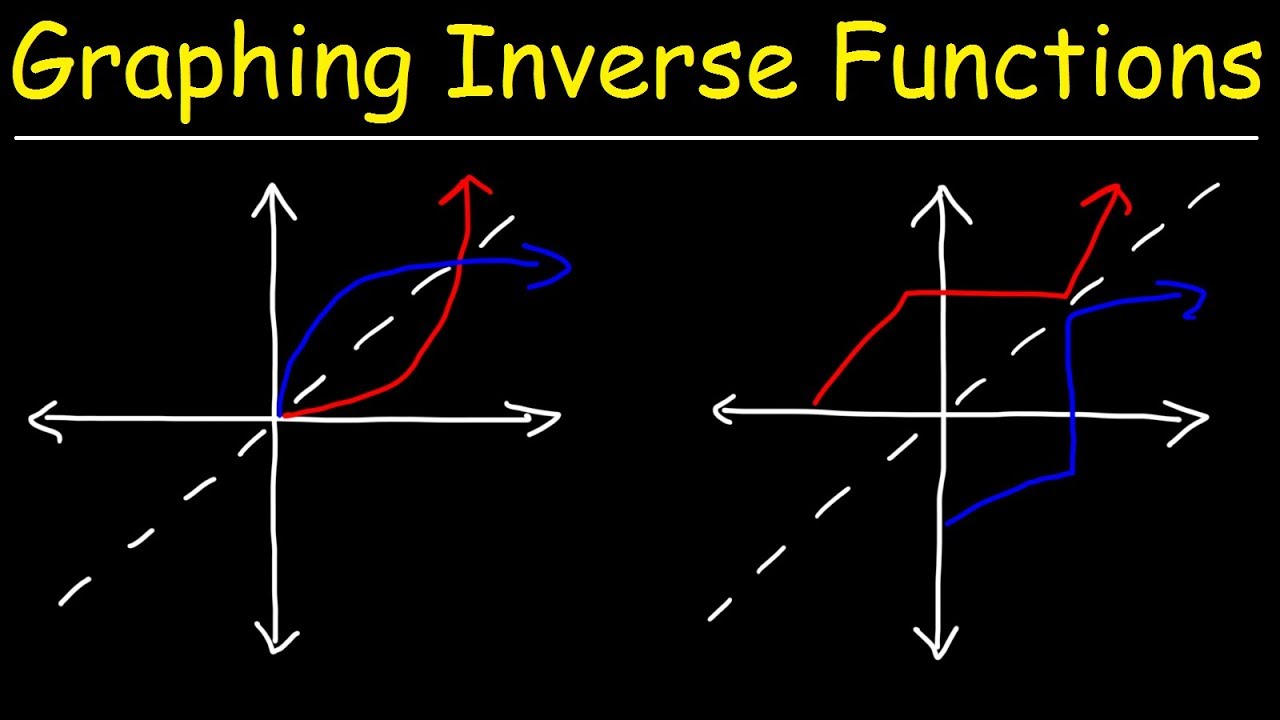
To graph the inverse function, one must first understand the relationship between a function and its inverse. The graph of the inverse function is a reflection of the original function across the line y = x. This reflection property not only aids in visualizing inverse functions but also provides a clear method for graphing them.
How to Graph the Inverse Function?
Graphing the inverse function can be broken down into a series of manageable steps. Here’s how you can approach it:
- Identify the original function: Start with the function you want to find the inverse for.
- Find the inverse function: Solve for y in terms of x to get the inverse function.
- Create a table of values: Select several x-values and compute their corresponding y-values for both the original and inverse functions.
- Plot the points: On a graph, plot the points for the original function and its inverse function.
- Reflect across y = x: Verify that the plotted points of the inverse are reflections of the original points across the line y = x.
- Draw the graph: Connect the points smoothly to create the graph for both functions.
Why Is It Important to Graph the Inverse Function?
Graphing the inverse function provides valuable visual insights into the behavior of both the original function and its inverse. This understanding is particularly useful in various fields, including:
- Mathematics: Analyzing the properties of functions and their inverses.
- Science: Applying mathematical concepts to real-world problems, such as calculating rates and measurements.
- Engineering: Designing systems that require inverse calculations, such as control systems.
What Are Some Common Challenges in Graphing Inverse Functions?
While the process of graphing inverse functions may seem straightforward, there can be challenges along the way. Some common issues include:
- Finding the inverse: Not all functions have inverses, and determining whether a function is one-to-one can be difficult.
- Graphing accuracy: Ensuring that points are accurately plotted and connected can be tricky, especially with complex functions.
- Understanding reflections: Visualizing the reflection across the line y = x may not be intuitive for some learners.
Are There Special Cases for Inverse Functions?
Yes, there are special cases that can affect the graphing of inverse functions. Some functions may not have inverses due to their nature, while others may have restricted domains to ensure they remain one-to-one. For example:
- Quadratic functions: These typically do not have inverses unless restricted to a specific domain.
- Trigonometric functions: The inverses of these functions, such as arcsin or arccos, require careful consideration of their ranges.
How Can Technology Assist in Graphing Inverse Functions?
In today's digital age, technology can greatly enhance the process of graphing inverse functions. Graphing calculators and software applications, such as Desmos or GeoGebra, provide interactive tools that simplify this task. Here’s how technology can assist:
- Visual Representation: Graphing software allows for easy visualization of both the original and inverse functions.
- Dynamic Manipulation: Users can manipulate equations and see real-time changes in the graph.
- Accuracy: Technology ensures precise calculations and plotting of points.
Conclusion: What Have We Learned About Graphing the Inverse Function?
Graphing the inverse function is a vital skill that involves understanding the relationship between functions and their inverses. Through the steps outlined in this article, the significance of graphing inverse functions becomes clear, not only in mathematical theory but also in practical applications. As you continue to practice and apply these concepts, you will find that the ability to graph the inverse function enhances your overall mathematical understanding and problem-solving prowess.
Embracing technology can further enrich your experience, making the process more engaging and efficient. Remember, the key to mastering how to graph the inverse function is practice and application. Happy graphing!
Understanding The Science Behind Ice Packs
Delightful Whipped Cream Frosting For Decorating Cakes
Clotrimazole Vs Lotrimin: Understanding The Key Differences